bienvenidos a mi blog, aqui podras encontrar informacion relacionada con el dibujo tecnico,
tales como proyecciones triedricas, circunferencias, espirales, entre otras cosas..... Adelante
Blog Educativo
lunes, 15 de junio de 2015
domingo, 14 de junio de 2015
Espirales
ESPIRALES
DEFINICIÓN:
La espiral es una curva plana que da vueltas alrededor de su centro alejándose cada vez más de él. A cada vuelta completa, la espiral se aleja de su centro a una distancia constante denominada "paso de la espiral".
Una espiral se define por los siguientes elementos:
Paso: Es la distancia longitudinal con que se desplaza un punto de la curva en una vuelta completa. Es decir, es la distancia entre dos espiras consecutivas.
Espira: Es la parte de la curva descrita en cada vuelta.
Núcleo: Es a partir de donde se genera, en expansión, la espiral. Los núcleos pueden ser lineales si los centros están situados en una línea, o poligonales si son los vértices del polígono los centros que generan la curva.
Radios vectores: Son la prolongación, bien de la línea donde están situados los centros del núcleo, o bien de los lados del polígono que hace de núcleo

Tipos de espirales
Las espirales bidimensionales más conocidas son:

La espiral de clotoide
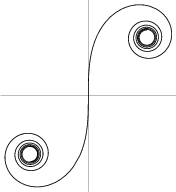
La espiral de Fermat

La espiral hiperbólica
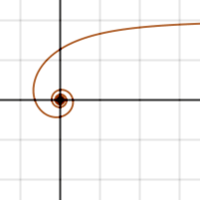
La espiral Logaritmica

¿Como Hacer Una Espiral?
Circunferencias
Circunferencias
La circunferencia es una línea curva cerrada cuyos puntos están todos a la misma distancia de un punto fijo llamado centro.
Elementos de la circunferencia
Centro de la circunferencia
El centro es el punto del que equidistan todos los puntos de la circunferencia.
Radio de la circunferencia
El radio es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma.
Cuerda
La cuerda es un segmento que une dos puntos de la circunferencia.
Diámetro
El diámetro es una cuerda que pasa por el centro de la circunferencia.
El diámetro mide el doble del radio.
Arco
Un arco es cada una de las partes en que una cuerda divide a la circunferencia.
Se suele asociar a cada cuerda el menor arco que delimita.
Semicircunferencia
Una semicircunferencia es cada uno de los arcos iguales que abarca un diámetro.
Ángulos de una circunferencia
Un ángulo, respecto de una circunferencia, pueden ser:
Ángulo central, si tiene su vértice en el centro de esta. Sus lados contienen a dos
radios.
La amplitud de un ángulo central es igual a la del arco que abarca.
Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados contienen dos
cuerdas.
La amplitud de un ángulo inscrito en una semi circunferencia equivale a la
mayor parte del ángulo exterior que limita dicha base. (Véase: arco capaz.)
Ángulo semi-inscrito, si su vértice es un punto de la circunferencia y sus
lados contienen una cuerda y una recta tangente a la circunferencia. El vértice
es el punto de tangencia.
La amplitud de un ángulo semi-inscrito es la mitad de la del arco que
abarca.
Ángulo interior, si su vértice está en el interior de la circunferencia.
La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la
del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones.
Ángulo exterior, si tiene su vértice en el exterior de la circunferencia
Lamina proyecciones triedricas
Lamina Proyecciones triedricas
- Se dividió la lamina en 4 partes iguales
- en el 1er cuadrante se trazo una linea con la medida deseada por nosotros de la cual desde la mitad se sacaron dos lineas inclinadas en forma de V
- se procedió a unir esas dos lineas con otras dos para que nos quedara una figura de rombo
- luego se nombraron las esquinas del rombo con las letras A,B,C,D, respectivamente
- se trazo una linea dividiendo el rombo en dos desde el punto A hasta el punto D
- En el 2do cuadrante se repitieron los pasos del 1er cuadrante , con la diferencia de que se trazo una segunda linea de B a C, quedando ahora el rombo dividido en 4.
- En el 3er cuadrante se repitieron los pasos del 2do cuadrante, pero ahora se trazaron dos lineas desde el punto A en forma de V hacia abajo cortando la linea B-C creando los puntos B y C respectivamente
- Igualmente se trozaron desde D dos lineas en forma de V las cuales cortaron a las recientemente trazadas creando los puntos O respectivamente, así como los puntos A y C como se puede observar en la imagen
- finalmente en el ultimo cuadrante se repitieron los pasos del 3ro, pero se la agregaron dos lineas curvas que se trazaron con el transportador desde A hasta B y desde C hasta D como se puede apreciar en las imágenes.
lunes, 25 de mayo de 2015
Proyecciones Triedricas
Proyecciones Triedricas
El sistema triedrico
Definición
Es un método de representación geométrico de los elementos del espacio tridimensional sobre un plano, es decir, la reducción de las tres dimensiones del espacio a las dos dimensiones del plano, utilizando una proyección ortogonal sobre dos planos que se cortan perpendicularmente. Para generar las vistas, uno de los planos se abate sobre el segundo.
Es un método gráfico de representación que consiste en obtener la imagen de un objeto (en planta y alzado), mediante la proyección de haces perpendiculares a dos planos principales de proyección, horizontal (PH) y vertical (PV). El objeto queda representado por su vista frontal (proyección en el plano vertical) y su vista superior (proyección en el plano horizontal); también se puede representar su vista lateral, como proyección auxiliar.
Si se prescinde de la línea de tierra, se denomina sistema diédrico directo.
¿Como se hace?
A este
tercer Plano sobre el que se Proyecta el Perfil del Objeto se le denomina Plano
de Perfil ( PP )
En este caso, la anotación del Punto
P va a ser una letra minúscula seguida de dos comas o comillas ( p´´ ).
La Proyección obtenida en el PP se
abatirá sobre el mismo Plano en el que se encuentran las dos Proyecciones
anteriores.
El Sistema Triédrico representa la
forma del objeto sobre tres Planos: Vertical, Horizontal y de Perfil. Es una
variante del Diédrico con la que se obtiene una mayor información del objeto a
representar.
Vamos a ver las distintas
Proyecciones que se pueden hacer de un objeto dentro del Sistema Triédrico.
Tipos
Son Cuatro:
1- Proyección del Punto.
2- Proyección de la Recta.
3- Proyección del Plano.
4- Proyección de Volúmenes ( iniciación a
la representación de Perspectivas ).
1 – Proyección del Punto.
La Proyección de un Punto sobre uno de los Planos de Proyección es la
intersección de la perpendicular al Plano, trazada desde ese Punto.
Si hacemos una prueba podemos ver: abatimos el PH haciendo que las
Proyecciones V y H formen un solo Plano. Entonces observamos que las
representaciones del Punto sobre estos dos Planos están sobre una misma Línea,
perpendicular a la Línea de tierra.
Como consecuencia, según la posición que ocupe el Punto en el espacio
respecto a los Planos de Proyección su Representación Gráfica variará.
2 – Proyección de la Recta.
Como ya sabemos una Recta queda determinada por dos Puntos. Para hallar las
Proyecciones de una Recta se determinan las Proyecciones de sus dos Puntos
sobre cada uno de los Planos de Proyección, uniéndolos entre sí. La Proyección
de la Recta sobre los Planos de Proyección PV y PH será siempre una línea
recta, excepto cuando sea perpendicular a uno de ellos ( en ese caso, su
representación sería un Punto ).
3 – Proyección del Plano.
En este apartado se deben de tener en cuenta que las Proyecciones
no son simplemente de Punto o Recta sobre Plano ( PH o PV ), sino de Plano sobre
Plano. Recuérdese, en primer lugar, que la intersección entre dos Planos es una
Línea Recta. Según esto, las Proyecciones de cada uno de los Planos se
representarán por las Líneas de intersección con sus Planos de Proyección.
4 – Proyección de Volúmenes.
Para hallar la Proyección de Volúmenes, se ha de aplicar lo explicado
anteriormente sobre las Proyecciones de Punto, Recta y Plano; hay que tener en
cuenta que un cuerpo se puede descomponer en un conjunto de Planos, que a su
vez están formados por Rectas y Puntos.
Fin
Suscribirse a:
Comentarios (Atom)










